Media Specialists
Understand Ad ROI Like A Pro
Our Media Mix Modelling course turns you into an ad spend guru, the Kiwi and Aussie way!
Products
Module 1: Marketing Mix Modelling Intro
$250 + gst per module
Know your instructor and their credentials. Delve into Marketing Mix Modelling history and principles. Feel confident about your course investment.

Module 2: The Art of Data Collection
250 + gst per module
Master data collection essentials. Learn what data to gather, how to format it, and pitfalls to avoid during the process.

Module 3: Excel Analysis Unleashed
250 + gst per module
Set up Excel Analysis ToolPak, run and interpret a correlation matrix, calculate adstocked media values, half-lives for media, and understand regression reports.
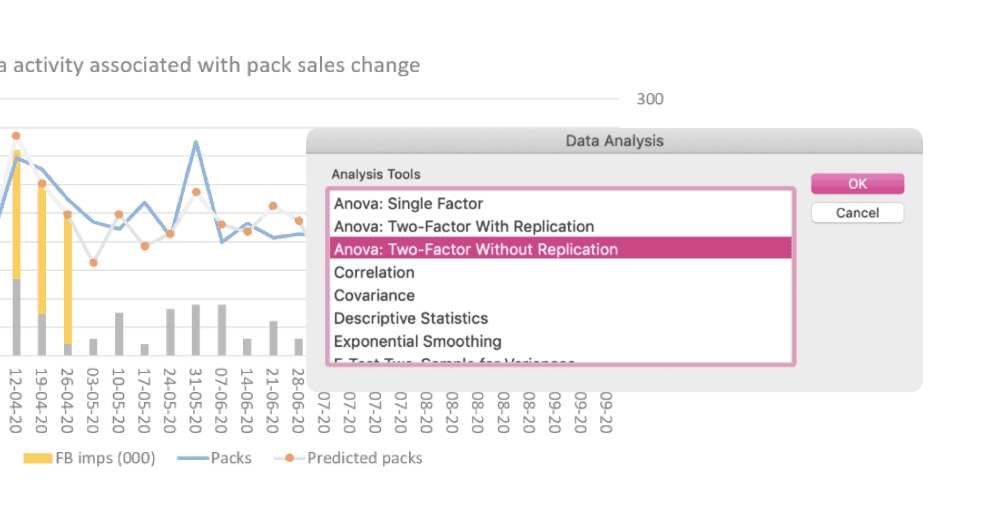
Module 4: Advanced Modelling Techniques
250 + gst per module
Understand confidence intervals, calculate ROI and price elasticity, deal with residuals, run a log-linear model, use quadratics to find optimal investment levels.
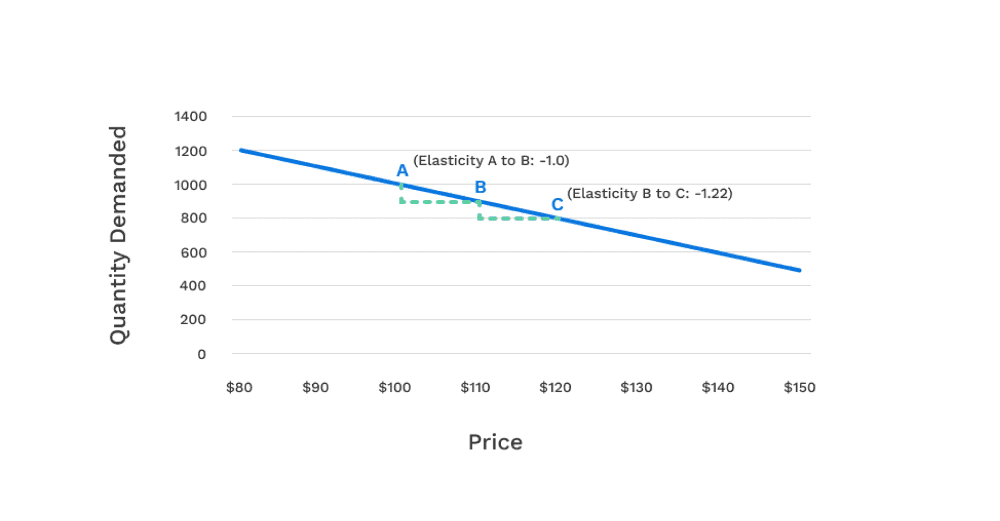
Module 5: Mastering Model Development
$250 + gst per module
Understand model development, calculate and plot prediction intervals, use LINEST and SOLVER, create a spreadsheet from your model, and explore chart options.

Solutions
Optimise Ad Spend
Struggling to allocate your advertising budget effectively? Our course teaches you Marketing Mix Modelling to ensure every dollar counts.

Level Up Your Marketing Skills
Marketers, stand out in your career. Our course in Marketing Mix Modelling helps you gain a key skill in today's marketing world.

Forecast More Accurately
Media agencies, use data and modelling to provide statistically-robust prediction models. Our course shows you how.

How it works
Free Consultation
Get in touch with Graham to discuss your needs, learn more about the course, and enrol.
Free Consultation
Get in touch with Graham to discuss your needs, learn more about the course, and enrol.
Access The Course
You will receive the full course videos and resources which you can complete at your own pace.
Access The Course
You will receive the full course videos and resources which you can complete at your own pace.
Need More Help?
Contact Graham with any questions or comments and subscribe to get access to the latest resources.
Need More Help?
Contact Graham with any questions or comments and subscribe to get access to the latest resources.
Features

Avoid Ad Waste
We help advertisers distinguish hits from misses. Learn to cut wasteful spend and amplify what works.

Media Negotiations
Promising TARPs or CPMs in a media proposal? Our course equips you to evaluate and negotiate better deals independently.

Supporting A Cause
We donate 10% of our profit to help mental health charities throughout New Zealand.